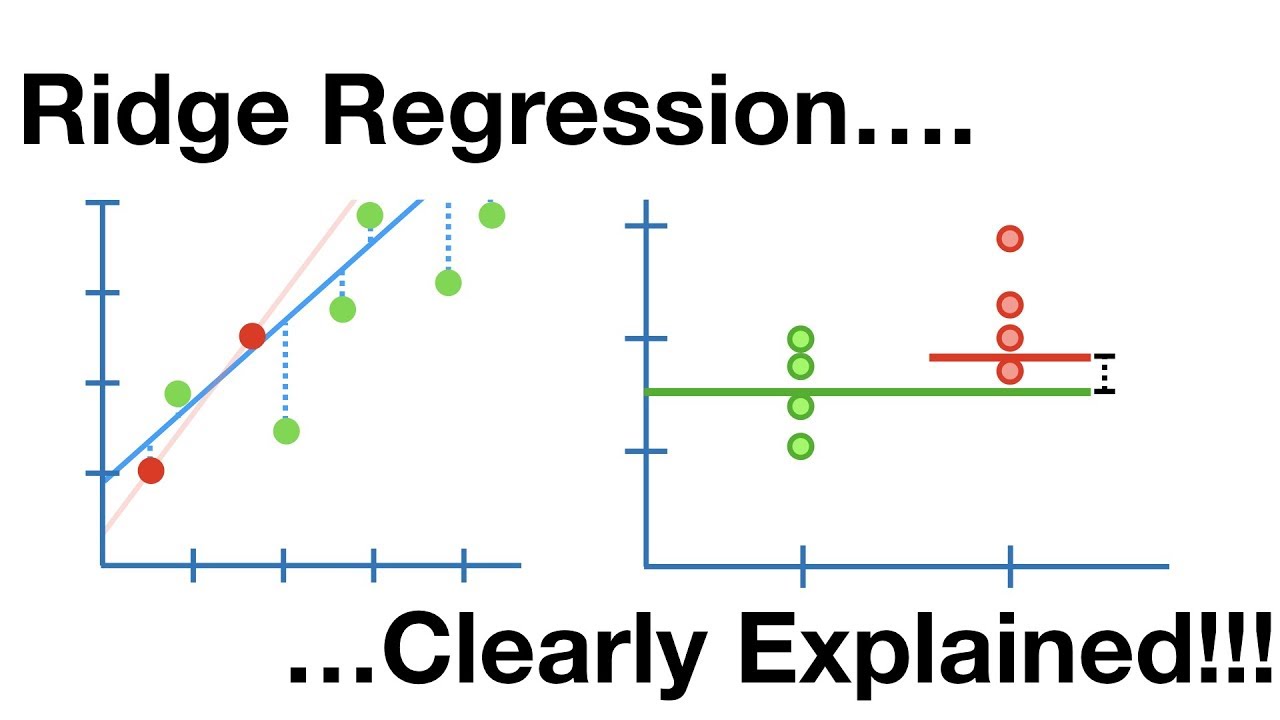
In layman’s terms, Ridge regression adds one more term to linear regression’s cost function to reduce error.
Ridge regression is a model-tuning method used to analyze data that suffer from multicollinearity. This method performs L2 regularization. When the issue of multicollinearity occurs, least-squares are unbiased, and variances are large; this results in predicted values being far away from the actual values.
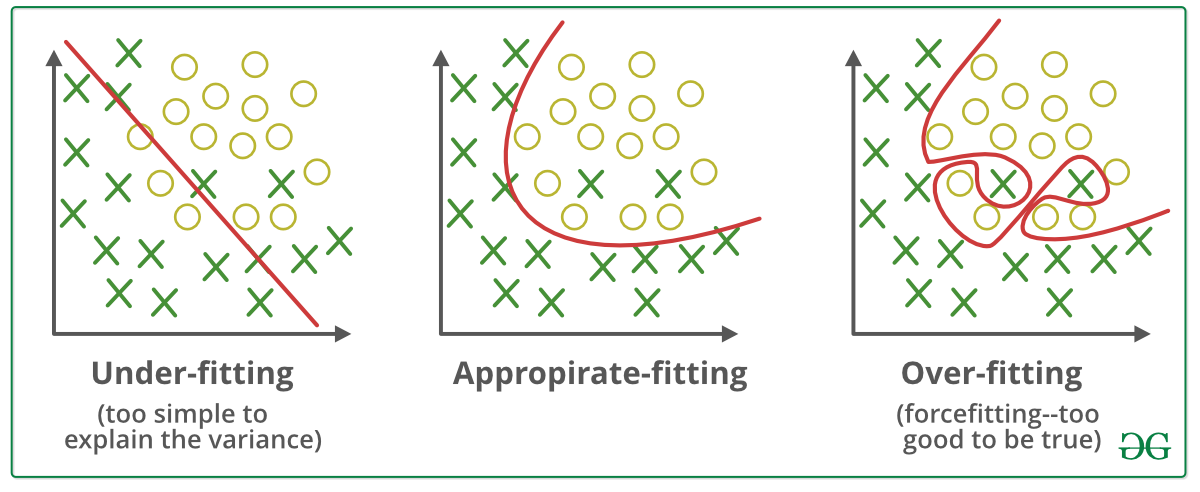
Before we jump into understanding bias and variance and the relation between them, we need first to understand Overfitting; it refers to a model which tries to capture the noise in data, i.e., it tries to memorize the trend in data perfectly, but the drawback in this is it might perform badly on the test dataset. This is because the model created fits exactly on the training dataset. So, if the model ever shows 100% accuracy for the training dataset, check for mistakes.
To do this, we can vary coefficients by using Regularization, i.e., remove the features which are not necessary or penalize the algorithm for wrong predictions and more errors.
Now to understand bias formally, it is stated as “the bias (or bias function) of an estimator is the difference between this estimator’s expected value and the true value of the parameter being estimated” this may sound too confusing in simpler terms; bias is said to be high when a model performs poorly on training data set.
Variance is stated as high when the model performs poorly on the test dataset.
In most of the scenarios, there will be a trade-off between Bias and Variance in any model we build.
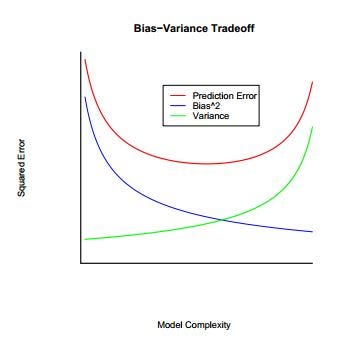
Look at the graph below, which shows the Variance and Bias for different Model Complexities. High Bias and Low Variance characterize a Low Complexity or Simple Model, whereas Low Bias and High Variance characterize a Highly Complex Model. Also, keep in mind that in both the very Simple Model and a highly Complex Model, the Total Error (Bias + Variance) of the model will be maximum.
Low bias and low variance will give a balanced model, whereas high bias leads to underfitting, and high variance lead to overfitting.
What is regularization?
When we use a regression model, it tries to predict the coefficients of various features of a dataset. Regularization tries to bring those coefficients close to 0, which reduces the complexity of the model and makes it more generalized for unforeseen data points. Which will reduce the model’s overfitting and bring down the total error
For example, if we consider OLS(ordinary least squares) or the residual sum of squares, it is given by
But if we observe it takes account only of the bias and not variance, the model will try to reduce the bias and overfit the data.
How does regularization help in reducing bias?
In regularization, we add a penalty term to the cost function, which reduces the model complexity that is, the cost function of the model reduces to OLS + Penalty
What is ridge regression?

In ridge regression penalty term is the product of the lambda parameter and the sum of the square of weights that is
If observed, this penalty term is known as Shrinkage Penalty. Lambda is known as the tuning parameter that is, if we consider the penalty to be zero, the bias will still be high, and the model will overfit if we make the penalty too high, the model will ignore the features, and the penalty term will prevail for example consider if we add 1 to infinity the change will be negligible similarly if the penalty term is too high the model will not take into consideration the feature coefficients.
Ridge regression does not cause sparsity.
Sparsity refers to when the coefficient of a feature drops to 0 that is, the feature becomes insignificant in the determination of the model
Ridge regression is also known as L2 regression since it uses the L2 norm for regularisation. In ridge regression, we strive to minimize the following function concerning”. As a result, we are attempting to reduce the following function:
The first term refers to the RSS or the residual sum square the second term is the penalty term which penalizes based on the square sum of the coefficients
For ease of solving, let p = 1
Expanding
The equation we get
For minima
at
Which, upon solving, results in
But for sparsity, this will happen when
Another type of overfitting prevention method, lasso regression, will be discussed in another release.
The main difference between the two is that Lasso regression is used if there are few variables, i.e., fewer predictors affect the output. In contrast, Ridge regression is effective when there are many parameters, i.e., most of them are significant.
This is because lasso regression eliminates some variables from the model, while ridge regression introduces a bias into the parameters to reduce variance.
There also exists a model called Elastic Net, a combination of Lasso and Ridge regression.
Tuning the Ridge Parameter: Exploring the Role of the Regularization Parameter in Ridge Regression
Exploring the Role of the Regularization Parameter in Ridge Regression
In Ridge Regression, the regularization parameter, often denoted as λ (lambda), plays a crucial role in controlling the balance between model complexity and overfitting. The regularization term added to the ordinary least squares objective function helps prevent overfitting by penalizing large coefficient values. Tuning the ridge parameter allows for adjusting the amount of regularization applied to the model.
The selection of the optimal ridge parameter involves finding a balance between bias and variance. A higher value of λ increases the regularization strength, shrinking the coefficients towards zero and reducing model complexity. This helps to mitigate the risk of overfitting but may increase bias. Conversely, a lower value of λ decreases regularization, allowing the model to fit the training data more closely but increasing the risk of overfitting and higher variance.
To find the appropriate ridge parameter, techniques such as cross-validation or grid search can be employed. Cross-validation helps evaluate the model’s performance across different values of λ and selects the value that minimizes the mean squared error or other evaluation metrics on validation data.
Handling Multicollinearity: Addressing the Issue of Multicollinearity in Ridge Regression
Multicollinearity refers to the presence of high correlation among predictor variables in a regression model. It can cause numerical instability and affect the interpretation of coefficients. Ridge Regression provides a solution for handling multicollinearity by adding a regularization term that reduces the impact of correlated predictors.
By introducing the ridge parameter, Ridge Regression ensures that the model’s coefficients are not excessively influenced by multicollinearity. The regularization term acts as a stabilizer by shrinking the coefficients towards zero. This helps alleviate the problem of large variances in coefficient estimates caused by multicollinearity.
Ridge Regression handles multicollinearity by reducing the impact of correlated predictors on the model’s output. Even though the coefficients may still be large, their contributions to the predictions are dampened. This allows the model to provide more reliable and stable estimates of the predictor effects.
Performance and Bias-Variance Tradeoff: Analyzing the Impact of Ridge Regression on Model Performance and the Bias-Variance Tradeoff
Ridge Regression has a direct impact on the bias-variance tradeoff, a fundamental concept in machine learning. The bias-variance tradeoff refers to the tradeoff between a model’s ability to fit the training data closely (low bias) and its ability to generalize well to unseen data (low variance).
In the context of Ridge Regression, the introduction of the regularization term increases bias by shrinking the coefficients. This bias helps reduce the risk of overfitting and improves the model’s generalization capabilities. However, as the regularization strength increases (higher λ values), the model’s flexibility decreases, resulting in higher bias.
On the other hand, Ridge Regression reduces variance by mitigating the influence of multicollinearity and preventing large coefficient estimates. By shrinking the coefficients towards zero, the regularization term stabilizes the model and reduces the variability in the predictions. This helps the model generalize better to unseen data and reduces the risk of overfitting.
Finding the optimal ridge parameter involves striking a balance between bias and variance. By tuning the regularization parameter, one can adjust the bias-variance tradeoff to achieve the best overall model performance.
Interpretability and Feature Selection: Considering the Effects of Ridge Regression on Interpretability and Feature Importance
Considering the Effects of Ridge Regression on Interpretability and Feature Importance
Ridge Regression has both advantages and challenges when it comes to interpretability and feature selection. Due to the regularization term, the coefficients in Ridge Regression tend to be smaller compared to ordinary least squares regression, which makes the interpretation of individual coefficients less straightforward. The shrinking effect of the regularization term can make it difficult to directly assess the importance of specific features based solely on their corresponding coefficients.
However, Ridge Regression still provides insights into feature importance through the magnitudes of the coefficients. Although the coefficients may be smaller, features with larger coefficients can still be considered more influential in the model’s predictions. It is important to note that interpretation should be done in the context of the regularization applied.
Feature selection is another aspect impacted by Ridge Regression. The regularization term naturally encourages the model to include all features in the analysis, albeit with smaller coefficients. Ridge Regression does not perform explicit feature selection by setting coefficients to exactly zero. However, the shrinking effect of the regularization can help implicitly prioritize important features by reducing the impact of less informative ones.
Extensions and Variations: Exploring Advanced Techniques and Variations of Ridge Regression
Ridge Regression has seen various extensions and variations that enhance its capabilities and address specific challenges. Some notable extensions include:
- Elastic Net Regression: Combines Ridge Regression with Lasso Regression to achieve a balance between L1 and L2 regularization. It provides both feature selection and coefficient shrinkage.
- Kernel Ridge Regression: Extends Ridge Regression to handle non-linear relationships by incorporating kernel functions. It allows for non-linear transformations of input variables.
- Bayesian Ridge Regression: Applies Bayesian principles to Ridge Regression by incorporating prior distributions on the coefficients. It provides a probabilistic framework for estimating coefficients and uncertainty.
- Sparse Ridge Regression: Combines Ridge Regression with a sparsity-inducing penalty, such as the L1 norm, to promote exact feature selection. It produces sparse solutions by setting some coefficients to zero.
Practical Applications: Examining Real-World Use Cases and Applications of Ridge Regression
Ridge Regression finds applications in various domains where predictive modeling and data analysis are crucial. Some common practical applications of Ridge Regression include:
Finance and Economics: Ridge Regression can be used for financial forecasting, portfolio optimization, and risk analysis. It helps model relationships between economic indicators, stock prices, and other financial variables.
Healthcare and Medicine: Ridge Regression aids in medical research, predicting disease outcomes, and analyzing medical data. It can be used to identify important risk factors and guide treatment decisions.
Marketing and Customer Analysis: Ridge Regression helps analyze customer behavior, predict customer preferences, and optimize marketing campaigns. It can identify key features that drive customer satisfaction and purchase decisions.
Environmental Sciences: Ridge Regression is applied to model environmental variables, such as climate patterns, pollution levels, and species distribution. It helps understand the relationships between various environmental factors and their impact on ecosystems.
By leveraging the regularization properties of Ridge Regression, these applications can benefit from improved predictive accuracy, handling multicollinearity, and extracting useful insights from complex datasets.
Conclusion
Ridge Regression is a powerful technique for regression analysis that addresses challenges such as multicollinearity and overfitting. It strikes a balance between bias and variance through the introduction of a regularization parameter, allowing for improved model generalization and stability. Although the interpretability of individual coefficients may be impacted, feature importance can still be inferred from their magnitudes. Extensions and variations of Ridge Regression offer further capabilities, catering to specific needs and scenarios.
In practical applications, Ridge Regression finds utility across domains such as finance, healthcare, marketing, and environmental sciences. It enables accurate predictions, helps identify influential features, and aids in decision-making processes.
FAQs
What is Ridge Regression, and how does it differ from ordinary linear regression?
Ridge Regression mitigates multicollinearity by adding a penalty term to shrink coefficients, unlike ordinary linear regression.
When should I consider using Ridge Regression?
Consider Ridge Regression for datasets with multicollinearity to stabilize estimates and improve model performance.
How does Ridge Regression address multicollinearity?
Ridge Regression penalizes large coefficients, effectively reducing their magnitude and mitigating multicollinearity’s impact.
What is the significance of the regularization parameter in Ridge Regression?
The regularization parameter controls coefficient shrinkage, allowing for a balance between bias and variance in the model.
How do I choose the optimal value of the regularization parameter?
The optimal value of the regularization parameter is typically chosen through techniques such as cross-validation. By evaluating the model’s performance across different values of the regularization parameter, one can select the value that minimizes prediction error.
Does Ridge Regression always improve model performance?
While Ridge Regression is effective in reducing the impact of multicollinearity and improving the stability of estimates, it may not always lead to better predictive performance. In some cases, other regression techniques may be more suitable.
Can Ridge Regression handle categorical variables?
Ridge Regression is primarily designed for numerical predictor variables. However, categorical variables can be incorporated by converting them into dummy variables (one-hot encoding) before applying Ridge Regression. It’s essential to ensure proper preprocessing of categorical variables to avoid issues with the interpretation of coefficients.