In supervised learning, overfitting is a major problem. When it comes to regression trees, it becomes more obvious to prevent this, we specify the Seth of the tree, but there is still a high chance of the dataset being overfitted. To avoid this, we use a random first regressor.
Before understanding how and why this algorithm prevents overfitting, we need to understand certain terms.
- Decision tree – form the base of the algorithm. As the name suggests decision tree creates a tree-like structure that asks a bunch of questions and tries to predict the result. In other words, it can be understood as a bucket load of nested if-else statements.
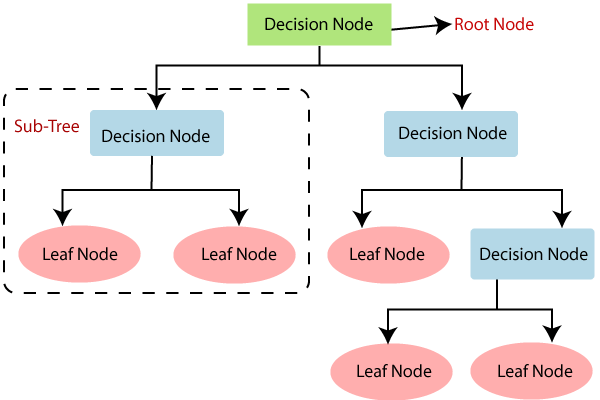
If we think the decision tree is highly sensitive to the input dataset, that is, it has high variance let’s understand using an example.
Notebook to test and run code: https://www.kaggle.com/code/tanavbajaj/random-forest/notebook
If we consider a random dataset like
| id | x1 | x2 | x3 | x4 | y |
| 1 | 2.33 | 4.3 | 3.31 | 8.99 | 5.4 |
| 2 | 2.5 | 5.9 | 6.47 | 10.16 | 7.8 |
| 3 | 1.61 | 9.9 | 3.02 | 11.29 | 1.2 |
| 4 | 8.39 | 7.6 | 2.15 | 7.56 | 4.4 |
| 5 | 4.26 | 9.9 | 4.79 | 5.97 | 10.2 |
| 6 | 3.35 | 1.9 | 8.79 | 7.88 | 10.6 |
| 7 | 5.29 | 2.8 | 7.05 | 8.05 | 4.9 |
| 8 | 9.74 | 4.0 | 1.17 | 4.14 | 8.7 |
| 9 | 6.6 | 2.8 | 4.17 | 11.0 | 11.0 |
| 10 | 2.08 | 6.4 | 3.18 | 11.01 | 3.6 |
| 11 | 8.36 | 2.6 | 4.76 | 12.94 | 11.9 |
| 12 | 9.74 | 1.5 | 7.44 | 14.82 | 8.9 |
| 13 | 1.02 | 6.1 | 8.83 | 13.84 | 1.5 |
| 14 | 9.05 | 6.6 | 5.36 | 8.64 | 1.4 |
| 15 | 7.89 | 2.2 | 5.31 | 5.26 | 7.3 |
| 16 | 6.44 | 2.9 | 4.02 | 14.46 | 8.1 |
| 17 | 5.94 | 9.4 | 5.05 | 2.94 | 8.5 |
| 18 | 4.12 | 9.1 | 9.4 | 2.23 | 6.7 |
| 19 | 7.71 | 1.1 | 5.98 | 7.29 | 1.8 |
| 20 | 4.97 | 1.4 | 6.49 | 12.96 | 11.1 |
And try to run the decision tree over it and generate the decision tree it might be something like
| x = data.iloc[:,1:5] y = data.iloc[:,-1] from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split( x, y, test_size=0.5,random_state=55)From sklearn.tree import DecisionTreeRegressor regressor = DecisionTreeRegressor(random_state=4,max_depth=2) from sklearn.tree import export_graphviz |
Now, if I swap the data x1 and x2 in rows 6, 7 ,8,9
| tmp = x.iloc[5:9,0].copy(deep=True)
x.iloc[5:9,0] = x.iloc[5:9,1] x.iloc[5:9,1] = tmp |
Upon retraining the model and generating the tree
| X_train, X_test, y_train, y_test = train_test_split( x, y, test_size=0.5,random_state=55)
regressor_second = DecisionTreeRegressor(random_state=4,max_depth=2) regressor_second.fit(X_train, y_train) export_graphviz(regressor_second, out_file =’tree2.dot’) with open(“tree2.dot”) as f: dot_graph = f.read() graphviz.Source(dot_graph).view() |
The tree changes to
This shows us that the decision tree is highly sensitive to the dataset.
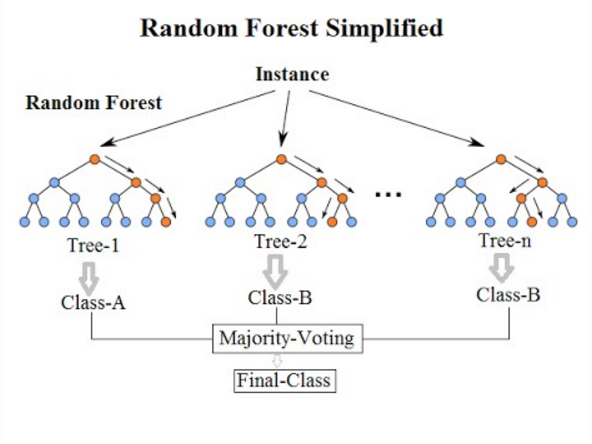
If we dive into a random forest, intuitively, it suggests that it might be some collection of trees, and this presumption is partially correct. A collection makes random forests of various decision trees. Now we may ask if we create trees using the same dataset, wouldn’t they all end up being the same and result in the same variance in the output? Here comes another term from the name into play that is Random. The algorithm uses a method of Bootstrapping. In bootstrapping, the algorithm randomly selects the subsets of the dataset over the number of iterations it is specified to.
To strengthen it more, it then uses another technique called Aggregation. In this, it randomly selects the number of specified features and generates the trees; what this does is it creates a large number of decision trees.
Some trees use the feature with more dominance, thus overfitting the dataset. In contrast, some trees use the worst combination of the feature and give the worst prediction in the result of all the trees being averaged out and predicted as the answer. This algorithm works on the principle of crowd wisdom.
Together the process of Bootstrapping and Aggregating is called Bagging.
As a result, in our random forest, we ended up with trees that employ distinct features for decision-making and were trained on various datasets (due to bagging).
Limitation of random forest
Extrapolation-
When we use the random forest, we often end up extrapolating the values far from the training dataset that is, if the dataset is not present in the training dataset, it will classify it all as the same.
Random forest’s key restriction is that many trees might render the process too sluggish and useless for real-time forecasts. These algorithms are generally quick to train but slow to generate predictions once trained. A more precise prediction needs more trees, resulting in a slower model. The random forest technique is fast enough for most real-world applications, but there may be cases when run-time speed is essential, and other approaches would be preferable.
